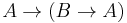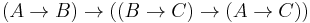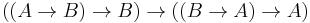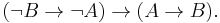Łukasiewicz logic
In mathematics, Łukasiewicz logic (English pronunciation: /luːkəˈʃɛvɪtʃ/, Polish pronunciation: [wukaˈɕɛvʲitʂ]) is a non-classical, many valued logic. It was originally defined in the early 20th-century by Jan Łukasiewicz as a three-valued logic;[1] it was later generalized to n-valued (for all finite n) as well as infinitely-many-valued variants, both propositional and first-order.[2] It belongs to the classes of t-norm fuzzy logics[3] and substructural logics.[4]
Contents |
Language
The propositional connectives of Łukasiewicz logic are implication 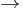 , negation
, negation 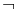 , equivalence
, equivalence  , weak conjunction
, weak conjunction 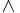 , strong conjunction
, strong conjunction  , weak disjunction
, weak disjunction 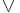 , strong disjunction
, strong disjunction  , and propositional constants
, and propositional constants 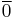 and
and 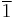 . The presence of weak and strong conjunction and disjunction is a common feature of substructural logics without the rule of contraction, to which Łukasiewicz logic belongs.
. The presence of weak and strong conjunction and disjunction is a common feature of substructural logics without the rule of contraction, to which Łukasiewicz logic belongs.
Axioms
The original system of axioms for propositional infinite-valued Łukasiewicz logic used implication and negation as the primitive connectives:
Propositional infinite-valued Łukasiewicz logic can also be axiomatized by adding the following axioms to the axiomatic system of monoidal t-norm logic:
- Divisibility:
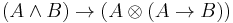
- Double negation:
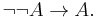
That is, infinite-valued Łukasiewicz logic arises by adding the axiom of double negation to basic t-norm logic BL, or by adding the axiom of divisibility to the logic IMTL.
Real-valued semantics
Infinite-valued Łukasiewicz logic is a real-valued logic in which sentences from sentential calculus may be assigned a truth value of not only zero or one but also any real number in between (e.g. 0.25). Valuations have a recursive definition where:
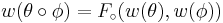 for a binary connective
for a binary connective 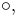
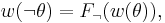
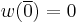 and
and 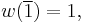
and where the definitions of the operations hold as follows:
- Implication:
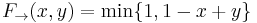
- Equivalence:
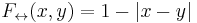
- Negation:

- Weak Conjunction:
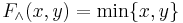
- Weak Disjunction:
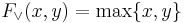
- Strong Conjunction:
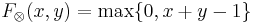
- Strong Disjunction:
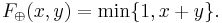
The truth function 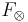 of strong conjunction is the Łukasiewicz t-norm and the truth function
of strong conjunction is the Łukasiewicz t-norm and the truth function 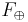 of strong disjunction is its dual t-conorm. The truth function
of strong disjunction is its dual t-conorm. The truth function 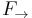 is the residuum of the Łukasiewicz t-norm. All truth functions of the basic connectives are continuous.
is the residuum of the Łukasiewicz t-norm. All truth functions of the basic connectives are continuous.
By definition, a formula is a tautology of infinite-valued Łukasiewicz logic if it evaluates to 1 under any valuation of propositional variables by real numbers in the interval [0, 1].
General algebraic semantics
The standard real-valued semantics determined by the Łukasiewicz t-norm is not the only possible semantics of Łukasiewicz logic. General algebraic semantics of propositional infinite-valued Łukasiewicz logic is formed by the class of all MV-algebras. The standard real-valued semantics is a special MV-algebra, called the standard MV-algebra.
Like other t-norm fuzzy logics, propositional infinite-valued Łukasiewicz logic enjoys completeness with respect to the class of all algebras for which the logic is sound (that is, MV-algebras) as well as with respect to only linear ones. This is expressed by the general, linear, and standard completeness theorems:[3]
- The following conditions are equivalent:
 is provable in propositional infinite-valued Łukasiewicz logic
is provable in propositional infinite-valued Łukasiewicz logic is valid in all MV-algebras (general completeness)
is valid in all MV-algebras (general completeness) is valid in all linearly ordered MV-algebras (linear completeness)
is valid in all linearly ordered MV-algebras (linear completeness) is valid in the standard MV-algebra (standard completeness).
is valid in the standard MV-algebra (standard completeness).
References
- ^ Łukasiewicz J., 1920, O logice trójwartościowej (in Polish). Ruch filozoficzny 5:170–171. English translation: On three-valued logic, in L. Borkowski (ed.), Selected works by Jan Łukasiewicz, North–Holland, Amsterdam, 1970, pp. 87–88. ISBN 0-7204-2252-3
- ^ Hay, L.S., 1963, Axiomatization of the infinite-valued predicate calculus. Journal of Symbolic Logic 28:77–86.
- ^ a b Hájek P., 1998, Metamathematics of Fuzzy Logic. Dordrecht: Kluwer.
- ^ Ono, H., 2003, "Substructural logics and residuated lattices — an introduction". In F.V. Hendricks, J. Malinowski (eds.): Trends in Logic: 50 Years of Studia Logica, Trends in Logic 20: 177–212.